A. METODE TERTUTUP
A.1. Metode Bagi-Dua
Metode Bagi-Dua adalah algoritma pencarian akar pada sebuah interval. Interval tersebut membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. Hal ini dilakukan berulang-ulang hingga diperoleh akar persamaan atau mendekati akar persamaan. Metode ini berlaku ketika ingin memecahkan persamaan f(x) = 0 dengan f merupakan fungsi kontinyu.
Prosedur Metode Bagi-Dua :
Misal
dijamin bahwa f(x) adalah fungsi kontinyu pada interval [a, b] dan
f(a)f(b) < 0. Ini artinya bahwa f(x) paling tidak harus memiliki akar
pada interval [a, b]. Kemudian definisikan titik tengah pada interval
[a, b] yaitu c :=  .
Dari sini kita memperoleh dua subinterval yaitu [a, c] dan [c, b].
Setelah itu, cek apakah f(a)f(c) < 0 atau f(b)f(c) < 0 ? Jika
f(a)f(c) < 0 maka b = c (artinya titik b digantikan oleh titik c yang
berfungsi sebagai titik b pada iterasi berikutnya), jika tidak maka a =
c. Dari iterasi pertama kita memperoleh interval [a, b] yang baru dan
titik tengah c yang baru. Kemudian lakukan pengecekan lagi seperti
sebelumnya sampai memperoleh error yang cukup kecil.
.
Dari sini kita memperoleh dua subinterval yaitu [a, c] dan [c, b].
Setelah itu, cek apakah f(a)f(c) < 0 atau f(b)f(c) < 0 ? Jika
f(a)f(c) < 0 maka b = c (artinya titik b digantikan oleh titik c yang
berfungsi sebagai titik b pada iterasi berikutnya), jika tidak maka a =
c. Dari iterasi pertama kita memperoleh interval [a, b] yang baru dan
titik tengah c yang baru. Kemudian lakukan pengecekan lagi seperti
sebelumnya sampai memperoleh error yang cukup kecil.
Contoh :
Carilah akar dari x3 + 4x2 – 10 = 0 pada interval [1, 2].
Penyelesaian :
Dalam penyelesaian ini saya akan menggunakan sampai iterasi ke-10 dan menggunakan 5 angka dibelakang koma.
f(x) = x3 + 4x2 – 10
f(1) = (1)3 + 4(1)2 – 10 = -5
f(2) = (2)3 + 4(2)2 – 10 = 14
f(1.5) = (1.5)3 + 4(1.5)2 – 10 = 2.375
f(1.25) = (1.25)3 + 4(1.25)2 – 10 = -1.79687
f(1.375) = (1.375)3 + 4(1.375)2 – 10 = 0.16210
f(1.3125) = (1.3125)3 + 4(1.3125)2 – 10 = -0.84838
f(1.34375) = (1.34375)3 + 4(1.34375)2 – 10 = -0.35098
f(1.35938) = (1.35938)3 + 4(1.35938)2 – 10 = -0.09632
f(1.36719) = (1.36719)3 + 4(1.36719)2 – 10 = 0.03239
f(1.36329) = (1.36329)3 + 4(1.36329)2 – 10 = -0.03200
f(1.36524) = (1.36524)3 + 4(1.36524)2 – 10 = 0.000016
f(1.36426) = (1.36426)3 + 4(1.36426)2 – 10 = -0.01601
f(1.36329) = (1.36329)3 + 4(1.36329)2 – 10 = -0.00784
n
|
a
|
B
|
c = (a + b)/2
|
f(a)
|
f(b)
|
f(c)
|
f(a)f(c)
|
f(b)f(c)
|
1
2
3
4
5
6
7
8
9
10
|
1
1
1.25
1.25
1.3125
1.34375
1.35938
1.35938
1.36329
1.36329
|
2
1.5
1.5
1.375
1.375
1.375
1.375
1.36719
1.36719
1.36524
|
1.5
1.25
1.375
1.3125
1.34375
1.35938
1.36719
1.36329
1.36524
1.36426
|
–
–
–
–
–
–
–
–
–
–
|
+
+
+
+
+
+
+
+
+
+
|
+
–
+
–
–
–
+
–
+
–
|
–
+
–
+
+
+
–
+
–
+
|
+
–
+
–
–
–
+
–
+
–
|
A.2. METODE REGULA FALSI
Metode Regular Falsi adalah panduan konsep dimulai dengan pemilihan dua titik awal x0 dan x1 sedemikian sehingga f(x0) dan f(x1) berlawanan tanda atau f(x0)f(x1) < 0. Kemudian menarik garis l dari titik f(x0) dan f(x1) sedemikian sehingga garis l berpotongan pada sumbu – x dan memotong kurva / grafik fungsi pada titik f(x0) dan f(x1). Sehingga Metode Regular Falsi ini akan menghasilkan titik potong pada sumbu-x yaitu x2 yang merupakan calon akar dan tetap berada dalam interval [x0, x1]. Metode ini kemudian berlanjut dengan menghasilkan berturut-turut interval [xn-1, xn] yang semuanya berisi akar f.

Prosedur Metode Regular Falsi
Menentukan interval titik awal x0 dan x1 sedemikian sehingga f(x0)f(x1)<0.
Setelah itu menghitung x2 = x1 –![\frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)} \frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_1%29%5Bx_1-x_0%5D%7D%7Bf%28x_1%29-f%28x_0%29%7D+&bg=ffffff&fg=666666&s=2) . Kemudian periksa apakah f(x0)f(x2) < 0 atau f(x1)f(x2) < 0, jika f(x0)f(x2) < 0 maka x0 = x0 atau x2 = x1, jika tidak maka x1 = x1 atau x2 = x0.
Kemudian ulangi terus langkah-langkah tersebut sampai ketemu ‘akar’
yang paling mendekati ‘akar yang sebenarnya’ atau mempunyai error yang
cukup kecil.
. Kemudian periksa apakah f(x0)f(x2) < 0 atau f(x1)f(x2) < 0, jika f(x0)f(x2) < 0 maka x0 = x0 atau x2 = x1, jika tidak maka x1 = x1 atau x2 = x0.
Kemudian ulangi terus langkah-langkah tersebut sampai ketemu ‘akar’
yang paling mendekati ‘akar yang sebenarnya’ atau mempunyai error yang
cukup kecil.
Setelah itu menghitung x2 = x1 –
Secara umum, rumus untuk Metode Regular Falsi ini adalah sebagai berikut
xn+1 = xn – ![\frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})} \frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_n%29%5Bx_n-x_%7Bn-1%7D%5D%7D%7Bf%28x_n%29-f%28x_%7Bn-1%7D%29%7D+&bg=ffffff&fg=666666&s=2)
Untuk mendapatkan rumus tersebut, perhatikan gambar diatas.
syarat : f(x0)f(x1) < 0
pandang garis l yang melalui (x0, f(x0)) dan (x1, f(x1)) sebagai gradien garis, sehingga diperoleh persamaan gradient sebagai berikut
karena x2 merupakan titik potong pada sumbu – x maka f(x2) = 0 = y, sehingga diperoleh
x1 – x2 = ![\frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)} \frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_1%29%5Bx_1-x_0%5D%7D%7Bf%28x_1%29-f%28x_0%29%7D+&bg=ffffff&fg=666666&s=2)
x2 = x1 – 
atau jika ditulis secara umum menjadi
xn+1 = xn – ![\frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})} \frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_n%29%5Bx_n-x_%7Bn-1%7D%5D%7D%7Bf%28x_n%29-f%28x_%7Bn-1%7D%29%7D+&bg=ffffff&fg=666666&s=2)
Contoh :
Tentukan akar dari 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Regular Falsi sampai 9 iterasi.
Penyelesaian :
f(x) = 4x3 – 15x2 + 17x – 6
iterasi 1 :
ambil x0 = -1 dan x1 = 3
f(-1) = 4(-1)3 – 15(-1)2 + 17(-1) – 6 = -42
f(3) = 4(3)3 – 15(3)2 + 17(3) – 6 = 18
x2 = (3) – ![\frac{(18)[3-(-1)]}{18-(-42)} \frac{(18)[3-(-1)]}{18-(-42)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-%28-1%29%5D%7D%7B18-%28-42%29%7D+&bg=ffffff&fg=666666&s=2) = 1.8
= 1.8
f(1.8) = 4(1.8)3 – 15(1.8)2 + 17(1.8) – 6 = -0.672
f(3) f(1.8) < 0 maka ambil x0 = x2 = 1.8 dan x1 = 3
iterasi 2 :
x2 = (3) – ![\frac{(18)[3-1.8]}{18-(-0.672)} \frac{(18)[3-1.8]}{18-(-0.672)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.8%5D%7D%7B18-%28-0.672%29%7D+&bg=ffffff&fg=666666&s=2) = 1.84319
= 1.84319
f(1.84319) = 4(1.84319)3 – 15(1.84319)2 + 17(1.84319) – 6 = -0.57817
f(3) f(1.84319) < 0 maka ambil x0 = x2 = 1.84319 dan x1 = 3
iterasi 3 :
x2 = (3) – ![\frac{(18)[3-1.84319]}{18-(-0.57817)} \frac{(18)[3-1.84319]}{18-(-0.57817)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.84319%5D%7D%7B18-%28-0.57817%29%7D+&bg=ffffff&fg=666666&s=2) = 1.87919
= 1.87919
f(1.87919) = 4(1.87919)3 – 15(1.87919)2 + 17(1.87919) – 6 = -0.47975
f(3) f(1.87919) < 0 maka ambil x0 = x2 = 1.87919 dan x1 = 3
iterasi 4 :
x2 = (3) – ![\frac{(18)[3-1.84319]}{18-(-0.47975)} \frac{(18)[3-1.84319]}{18-(-0.47975)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.84319%5D%7D%7B18-%28-0.47975%29%7D+&bg=ffffff&fg=666666&s=2) = 1.90829
= 1.90829
f(1.90829) = 4(1.90829)3 – 15(1.90829)2 + 17(1.90829) – 6 = -0.38595
f(3) f(1.90829) < 0 maka ambil x0 = x2 = 1.90829 dan x1 = 3
iterasi 5 :
x2 = (3) – ![\frac{(18)[3-1.90829]}{18-(-0.38595)} \frac{(18)[3-1.90829]}{18-(-0.38595)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.90829%5D%7D%7B18-%28-0.38595%29%7D+&bg=ffffff&fg=666666&s=2) = 1.93120
= 1.93120
f(1.93120) = 4(1.93120)3 – 15(1.93120)2 + 17(1.93120) – 6 = -0.30269
f(3) f(1.93120) < 0 maka ambil x0 = x2 = 1.93120 dan x1 = 3
iterasi 6 :
x2 = (3) – ![\frac{(18)[3-1.93120]}{18-(-0.30269)} \frac{(18)[3-1.93120]}{18-(-0.30269)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.93120%5D%7D%7B18-%28-0.30269%29%7D+&bg=ffffff&fg=666666&s=2) = 1.94888
= 1.94888
f(1.94888) = 4(1.94888)3 – 15(1.94888)2 + 17(1.94888) – 6 = -0.23262
f(3) f(1.94888) < 0 maka ambil x0 = x2 = 1.94888 dan x1 = 3
iterasi 7 :
x2 = (3) – ![\frac{(18)[3-1.94888]}{18-(-0.23262)} \frac{(18)[3-1.94888]}{18-(-0.23262)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.94888%5D%7D%7B18-%28-0.23262%29%7D+&bg=ffffff&fg=666666&s=2) = 1.96229
= 1.96229
f(1.96229) = 4(1.96229)3 – 15(1.96229)2 + 17(1.96229) – 6 = -0.17597
f(3) f(1.96229) < 0 maka ambil x0 = x2 = 1.96229 dan x1 = 3
iterasi 8 :
x2 = (3) – ![\frac{(18)[3-1.96229]}{18-(-0.17597)} \frac{(18)[3-1.96229]}{18-(-0.17597)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.96229%5D%7D%7B18-%28-0.17597%29%7D+&bg=ffffff&fg=666666&s=2) = 1.97234
= 1.97234
f(1.97234) = 4(1.97234)3 – 15(1.97234)2 + 17(1.97234) – 6 = -0.13152
f(3) f(1.97234) < 0 maka ambil x0 = x2 = 1.97234 dan x1 = 3
iterasi 9 :
x2 = (3) – ![\frac{(18)[3-1.97234]}{18-(-0.13152)} \frac{(18)[3-1.97234]}{18-(-0.13152)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-1.97234%5D%7D%7B18-%28-0.13152%29%7D+&bg=ffffff&fg=666666&s=2) = 1.97979
= 1.97979
n
|
x0
|
x1
|
x1
|
f(x0)
|
f(x1)
|
f(x2)
|
1
2
3
4
5
6
7
8
9
|
-1
1.8
1.84319
1.87919
1.90829
1.93120
1.94888
1.96229
1.97234
|
3
3
3
3
3
3
3
3
3
|
1.8
1.84319
1.87919
1.90829
1.93120
1.94888
1.96229
1.97234
1.97979
|
-42
-0.672
-0.57817
-0.47975
-0.38595
-0.30269
-0.23262
-0.17597
-0.13152
|
18
18
18
18
18
18
18
18
18
|
-0.672
-0.57817
-0.47975
-0.38595
-0.30269
-0.23262
-0.17597
-0.13152
-0.09741
|
A. METODE TERBUKA
B.1. Metode Titik Tetap
Metode Titik Tetap adalah suatu metode pencarian akar suatu fungsi f(x) secara sederhana dengan menggunakan satu titik awal. Perlu diketahui bahwa fungsi f(x) yang ingin dicari hampiran akarnya harus konvergen. Misal x adalah Fixed Point (Titik Tetap) fungsi f(x) bila g(x) = x dan f(x) = 0.
Teorema :
Diketahui g(x) fungsi kontinu dan {Xn} adalah barisan yang terbetuk oleh Fixed Point Iteration, maka
Jika  Xn = x maka x adalah Fixed Point fungsi g(x).
Xn = x maka x adalah Fixed Point fungsi g(x).
Sumber gambar : karlcalculus
Prosedur Metode Titik Tetap
Misal
f(x) adalah fungsi yang konvergen dengan f(x) = 0, maka untuk mencari
nilai akarnya atau hampiran akarnya kita terlebih dahulu mengubah
kedalam bentuk x = g(x). Kemudian tentukan nilai titik awal, misal x1. Setelah itu disubstitusikan titik awalnya ke persamaan g(x) sedemikian sehingga g(x1) = x2, setelah itu titik x2 yang diperoleh substitusikan lagi ke g(x) sedemikian sehingga g(x2) = x3. Jadi apabila ditulis iterasinya akan menjadi
x1 (penetuan titik awal)
x2 = g(x1) (iterasi pertama)
x3 = g(x2) (iterasi kedua)
.
.
.
xn = g(xn-1) (iterasi ke-n)
Iterasi ini akan berhenti jika x = g(x) dan f(x) = 0 atau sudah mencapai nilai error yang cukup kecil (|xn – xn-1| <  ).
).
Contoh :
Selesaikan persamaan x – e-x = 0 dengan menggunakan Fixed Point dengan 10 iterasi atau sampai dua angka dibelakang koma tidak berubah.
Penyelesaian :
f(x) = x – e-x
ubah terlebih dahulu kedalam bentuk x = g(x), sehingga diperoleh x = e-x
misal kita ambil titik awalnya x1 = 0.5, maka iterasinya adalah xn+1 = e-x_{n} akan diperoleh
x1 = 0.5 (penetuan titik awal)
f(x1) = 0.5 – e-0.5 = -0.1065
x2 = g(x1) = e-0.5 = 0.6065 (iterasi pertama)
f(x1) = 0.6065 – e-0.6065 = 0.0612
x3 = g(x2) = e-0.6065 = 0.5452 (iterasi ke-2)
f(x1) = 0.5452 – e-0.5452 = -0.0345
x4 = g(x3) = e-0.5452 = 0.5797 (iterasi ke-3)
f(x1) = 0.5797 – e-0.5797 = 0.0196
.
.
.
x9 = g(x8) e-0.5664 = 0.5675 (iterasi ke-9)
f(x1) = 0.5 – e-0.5 = -0.1065
x10 = g(x9) e-0.5675 = 0.5669 (iterasi ke-10)
f(x1) = 0.5 – e-0.5 = -0.1065
sehingga apabila ditulis dalam bentuk table akan diperoleh
n
|
xn
|
g(xn-1)
|
f(xn)
|
1
2
3
4
5
6
7
8
9
10
|
0.5
0.6065
0.5452
0.5797
0.5600
0.5712
0.5648
0.5684
0.5664
0.5675
|
0.6065
0.5452
0.5797
0.5600
0.5712
0.5648
0.5684
0.5664
0.5675
0.5669
|
-0.1065
0.0612
-0.0345
0.0196
-0.0112
0.0006
-0.0003
0.00019
-0.00011
0.00005
|
Jadi hampiran akar yang diperoleh menggunakan Fixed Point adalah 0.5675
Contoh 2 :
Hitunglah hampiran akar dari persamaan x2 – 2x – 3 = 0 pada interval [1, 4] menggunakan Fixed Point.
Penyelesaian :
Misal persamaan x2 – 2x – 3 = 0 diubah menjadi x(x – 2) – 3 = 0 sehingga diperoleh x =  dan iterasinya menjadi xn+1 =
dan iterasinya menjadi xn+1 =  . ambil titik awal x1 = 4.
. ambil titik awal x1 = 4.
Sehingga apabila ditulis dalam tabel diperoleh :
n
|
xn
|
g(xn-1)
|
f(xn)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
4
1.5
-6
-0.375
-1.2631
-0.9193
-1.0276
-0.9908
-1.003
-0.999
-1.00033
-0.9989
-1.00036
-0.99988
-1.00004
-0.99998
-1.00001
-0.99999
-1.00000
|
1.5
-6
-0.375
-1.2631
-0.9193
-1.0276
-0.9908
-1.003
-0.999
-1.00033
-0.9989
-1.00036
-0.99988
-1.00004
-0.99998
-1.00001
-0.99999
-1.00000
-1.00000
|
5
-3.75
45
-2.1093
1.1216
-0.3162
0.1111
-0.0367
0.012
-0.00039
0.00013
-0.00043
0.00014
-0.00004
0.000016
-0.000008
0.00004
-0.000004
0
|
Jadi akar dari f(x) = x2 – 2x – 3 = 0 adalah -1
Sekarang bagaimana jika fungsi pada Contoh 2 kita ubah menjadi x =  ? Berapa nilai akarnya? Pada kasus ini jika menggunakan Fixed Point
maka kita tidak akan menemukan hampiran akarnya karena fungsi tersebut
divergen. Bagaimana cara kita bisa menentukan bahwa fungsi tersebut
divergen atau konvergen? Perhatikan teorema dibawah ini.
? Berapa nilai akarnya? Pada kasus ini jika menggunakan Fixed Point
maka kita tidak akan menemukan hampiran akarnya karena fungsi tersebut
divergen. Bagaimana cara kita bisa menentukan bahwa fungsi tersebut
divergen atau konvergen? Perhatikan teorema dibawah ini.
Teorema :
Diketahui g kontinu pada [a, b] dan paling sedikit memiliki satu akar pada [a, b] jika |g'(x)|  M < 1,
M < 1, 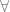 x
x  [a, b] maka iterasi xn+1 = g(xn) dengan xi
[a, b] maka iterasi xn+1 = g(xn) dengan xi  [a, b] menghasilkan barisan {Xn} konvergen yaitu
[a, b] menghasilkan barisan {Xn} konvergen yaitu  xn = L
xn = L  {Xn}
{Xn} 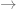 0
0
x =  = g(x)
= g(x)
g'(x) = 3x2, dimana 3x2  0, maka menurut Teorema diatas g(x) divergen.
0, maka menurut Teorema diatas g(x) divergen.
INGAT : dalam Fixed Point, g(x) harus konvergen. Jika divergen, maka tidak bisa dilakukan perhitungan akar menggunakan Fixed Point ini
B.2. METODE NEWTON RAPHSON
Metode Newton-Raphson
adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu
titik, dimana fungsi f(x) mempunyai turunan. Metode ini dianggap lebih
mudah dari Metode Bagi-Dua
(Bisection Method) karena metode ini menggunakan pendekatan satu titik
sebagai titik awal. Semakin dekat titik awal yang kita pilih dengan akar
sebenarnya, maka semakin cepat konvergen ke akarnya.
Prosedur Metode Newton :
menentukan x0 sebagai titik awal, kemudian menarik garis lurus (misal garis l) yang menyinggung titik f(x0). Hal ini berakibat garis l memotong sumbu – x di titik x1. Setelah itu diulangi langkah sebelumnya tapi sekarang x1 dianggap sebagai titik awalnya. Dari mengulang langkah-langkah sebelumnya akan mendapatkan x2, x3, … xn dengan xn yang diperoleh adalah bilangan riil yang merupakan akar atau mendekati akar yang sebenarnya.
Perhatikan gambar diatas untuk menurunkan rumus Metode Newton-Raphson
persamaan garis l : y – y0 = m(x – x0)
y – f(x0) = f'(x0)(x – x0)
x1 adalah perpotongan garis l dengan sumbu – x
0 – f(x0) = f'(x0)(x1 – x0)
y = 0 dan x = x1 maka koordinat titik (x1, 0)
–  = (x1 – x0)
= (x1 – x0)
x1 = x0 – 
x2 = x1 – 
.
.
.
xn = xn-1–  untuk n = 1, 2, 3, …
untuk n = 1, 2, 3, …
Contoh :
Tentukan akar dari persamaan 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Newton-Raphson.
Penyelesaian :
f(x) = 4x3 – 15x2 + 17x – 6
f’(x) = 12x2 – 30x + 17
iterasi 1 :
ambil titik awal x0 = 3
f(3) = 4(3)3 – 15(3)2 + 17(3) – 6 = 18
f’(3) = 12(3)2 – 30(3) + 17 = 35
x1 = 3 – 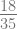 = 2.48571
= 2.48571
iterasi 2 :
f(2.48571) = 4(2.48571)3 – 15(2.48571)2 + 17(2.48571) – 6 = 5.01019
f’(2.48571) = 12(2.48571)2 – 30(2.48571) + 17 = 16.57388
x2 = 2.48571 – 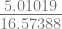 = 2.18342
= 2.18342
iterasi 3 :
f(2.18342) = 4(2.18342)3 – 15(2.18342)2 + 17(2.18342) – 6 = 1.24457
f’(2.18342) = 12(2.18342)2 – 30(2.18342) + 17 = 8.70527
x3 = 2.18342 – 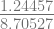 = 2.04045
= 2.04045
iterasi 4 :
f(2.04045) = 4(2.04045)3 – 15(2.04045)2 + 17(2.04045) – 6 = 0.21726
f’(2.04045) = 12(2.04045)2 – 30(2.04045) + 17 = 5.74778
x4 = 2.04045 – 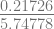 = 2.00265
= 2.00265
iterasi 5 :
f(3) = 4(2.00265)3 – 15(2.00265)2 + 17(2.00265) – 6 = 0.01334
f’(2.00265) = 12(2.00265)2 – 30(2.00265) + 17 = 5.04787
x5 = 2.00265 – 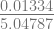 = 2.00001
= 2.00001
iterasi 6 :
f(2.00001) = 4(2.00001)3 – 15(2.00001)2 + 17(2.00001) – 6 = 0.00006
f’(2.00001) = 12(2.00001)2 – 30(2.00001) + 17 = 5.00023
x6 = 2.00001 – 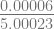 = 2.00000
= 2.00000
iterasi 7 :
f(2) = 4(2)3 – 15(2)2 + 17(2) – 6 = 0
jika disajikan dalam tabel, maka seperti tabel dibawah ini.
n
|
xn
|
f(xn)
|
f'(xn)
|
0
1
2
3
4
5
6
|
3
2.48571
2.18342
2.04045
2.00265
2.00001
2.00000
|
18
5.01019
1.24457
0.21726
0.01334
0.00006
0.00000
|
35
16.57388
8.70527
5.74778
5.04787
5.00023
5.00000
|
B.3. METODE SECANT
Pada Metode Newton-Raphson
memerlukan syarat wajib yaitu fungsi f(x) harus memiliki turunan f'(x).
Sehingga syarat wajib ini dianggap sulit karena tidak semua fungsi bisa
dengan mudah mencari turunannya. Oleh karena itu muncul ide dari yaitu
mencari persamaan yang ekivalen dengan rumus turunan fungsi. Ide ini
lebih dikenal dengan nama Metode Secant. Ide dari metode ini yaitu menggunakan gradien garis yang melalui titik (x0, f(x0)) dan (x1, f(x1)). Perhatikan gambar dibawah ini.
Persamaan garis l adalah
Karena x = x2 maka y = 0, sehingga diperoleh
x2 – x1 = ![-\frac{f(x_1)[x_0-x_1]}{f(x_0)-f(x_1)} -\frac{f(x_1)[x_0-x_1]}{f(x_0)-f(x_1)}](https://s0.wp.com/latex.php?latex=-%5Cfrac%7Bf%28x_1%29%5Bx_0-x_1%5D%7D%7Bf%28x_0%29-f%28x_1%29%7D+&bg=ffffff&fg=666666&s=2)
x2 = x1 – ![\frac{f(x_1)[x_0-x_1]}{f(x_0)-f(x_1)} \frac{f(x_1)[x_0-x_1]}{f(x_0)-f(x_1)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_1%29%5Bx_0-x_1%5D%7D%7Bf%28x_0%29-f%28x_1%29%7D+&bg=ffffff&fg=666666&s=2)
= x1 – ![\frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)} \frac{f(x_1)[x_1-x_0]}{f(x_1)-f(x_0)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_1%29%5Bx_1-x_0%5D%7D%7Bf%28x_1%29-f%28x_0%29%7D+&bg=ffffff&fg=666666&s=2)
secara umum rumus Metode Secant ini ditulis
xn+1 = xn – ![\frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})} \frac{f(x_n)[x_n-x_{n-1}]}{f(x_n)-f(x_{n-1})}](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bf%28x_n%29%5Bx_n-x_%7Bn-1%7D%5D%7D%7Bf%28x_n%29-f%28x_%7Bn-1%7D%29%7D+&bg=ffffff&fg=666666&s=2)
Prosedur Metode Secant :
Ambil dua titik awal, misal x0 dan x1. Ingat bahwa pengambilan titik awal tidak disyaratkan alias pengambilan secara sebarang. Setelah itu hitung x2 menggunakan rumus diatas. Kemudian pada iterasi selanjutnya ambil x1 dan x2 sebagai titik awal dan hitung x3. Kemudian ambil x2 dan x3 sebagai titik awal dan hitung x4. Begitu seterusnya sampai iterasi yang diingankan atau sampai mencapai error yang cukup kecil.
Contoh :
Tentukan salah satu akar dari 4x3 – 15x2 + 17x – 6 = 0 menggunakan Metode Secant sampai 9 iterasi.
Penyelesaian :
f(x) = 4x3 – 15x2 + 17x – 6
iterasi 1 :
ambil x0 = -1 dan x1 = 3 (ngambil titik awal ini sebarang saja, tidak ada syarat apapun)
f(-1) = 4(-1)3 – 15(-1)2 + 17(-1) – 6 = -42
f(3) = 4(3)3 – 15(3)2 + 17(3) – 6 = 18
x2 = (3) – ![\frac{(18)[3-(-1)]}{18-(-42)} \frac{(18)[3-(-1)]}{18-(-42)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%2818%29%5B3-%28-1%29%5D%7D%7B18-%28-42%29%7D+&bg=ffffff&fg=666666&s=2) = 1.8
= 1.8
iterasi 2 :
ambil x1 = 3 dan x2 = 1.8
f(1.8) = 4(1.8)3 – 15(1.8)2 + 17(1.8) – 6 = -0.672
x3 = (1.8) – ![\frac{(-0.672)[1.8-(3)]}{-0.672-18} \frac{(-0.672)[1.8-(3)]}{-0.672-18}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%28-0.672%29%5B1.8-%283%29%5D%7D%7B-0.672-18%7D+&bg=ffffff&fg=666666&s=2) = 1.84319
= 1.84319
iterasi 3 :
ambil x2 = 1.8 dan x3 = 1.84319
f(1.84319) = 4(1.84319)3 – 15(1.84319)2 + 17(1.84319) – 6 = -0.57817
x4 = (1.84319) – ![\frac{(-0.57817)[1.84319-1.8]}{-0.57817-(0.672)} \frac{(-0.57817)[1.84319-1.8]}{-0.57817-(0.672)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%28-0.57817%29%5B1.84319-1.8%5D%7D%7B-0.57817-%280.672%29%7D+&bg=ffffff&fg=666666&s=2) = 2.10932
= 2.10932
iterasi 4 :
ambil x3 = 1.84319 dan x4 = 2.10932
f(2.10932) = 4(2.10932)3 – 15(2.10932)2 + 17(2.10932) – 6 = 0.65939
x5 = (2.10932) – ![\frac{(0.65939)[2.10932-1.84319]}{0.65939-(-0.57817)} \frac{(0.65939)[2.10932-1.84319]}{0.65939-(-0.57817)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%280.65939%29%5B2.10932-1.84319%5D%7D%7B0.65939-%28-0.57817%29%7D+&bg=ffffff&fg=666666&s=2) = 1.96752
= 1.96752
iterasi 5 :
ambil x4 = 2.10932 dan x5 = 1.96752
f(1.96752) = 4(1.96752)3 – 15(1.96752)2 + 17(1.96752) – 6 = -0.15303
x6 = (1.96752) – ![\frac{(-0.15303)[1.96752-2.10932]}{-0.15303-0.65939)} \frac{(-0.15303)[1.96752-2.10932]}{-0.15303-0.65939)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%28-0.15303%29%5B1.96752-2.10932%5D%7D%7B-0.15303-0.65939%29%7D+&bg=ffffff&fg=666666&s=2) = 1.99423
= 1.99423
iterasi 6 :
ambil x5 = 1.96752 dan x6 = 1.99423f(1.99423) = 4(1.99423)3 – 15(1.99423)2 + 17(1.99423) – 6 = -0.02854
x7 = (1.99423) – ![\frac{(-0.02854)[1.99423-1.96752]}{-0.02854-(-0.15303)} \frac{(-0.02854)[1.99423-1.96752]}{-0.02854-(-0.15303)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%28-0.02854%29%5B1.99423-1.96752%5D%7D%7B-0.02854-%28-0.15303%29%7D+&bg=ffffff&fg=666666&s=2) = 2.00036
= 2.00036
iterasi 7 :
ambil x6 = 1.99423 dan x7 = 2.00036
f(2.00036) = 4(2.00036)3 – 15(2.00036)2 + 17(2.00036) – 6 = 0.00178
x8 = (2.00036) – ![\frac{(0.00178)[2.00036-1.99423]}{0.00178-(-0.02854)} \frac{(0.00178)[2.00036-1.99423]}{0.00178-(-0.02854)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%280.00178%29%5B2.00036-1.99423%5D%7D%7B0.00178-%28-0.02854%29%7D+&bg=ffffff&fg=666666&s=2) = 2.00000
= 2.00000
iterasi 8 :
ambil x7 = 2.00036 dan x8 = 1.999996
f(1.999996) = 4(1.999996)3 – 15(1.999996)2 + 17(1.999996) – 6 = -0.0002
x9 = (1.999996) – ![\frac{(-0.0002)[1.999996-2.00036]}{-0.0002-0.00178} \frac{(-0.0002)[1.999996-2.00036]}{-0.0002-0.00178}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%28-0.0002%29%5B1.999996-2.00036%5D%7D%7B-0.0002-0.00178%7D+&bg=ffffff&fg=666666&s=2) = 2.0000
= 2.0000
iterasi 9 :
ambil x8 = 1.999996 dan x9 = 2.00000
f(2.00000) = 4(2.00000)3 – 15(2.00000)2 + 17(2.00000) – 6 = 0.00000
x10 = (2.00000) – ![\frac{(0.00000)[2.00000-1.999996]}{0.00000-(-0.00002)} \frac{(0.00000)[2.00000-1.999996]}{0.00000-(-0.00002)}](https://s0.wp.com/latex.php?latex=%5Cfrac%7B%280.00000%29%5B2.00000-1.999996%5D%7D%7B0.00000-%28-0.00002%29%7D+&bg=ffffff&fg=666666&s=2) = 0.00000
= 0.00000
n
|
xn-1
|
xn
|
xn+1
|
f(xn-1)
|
f(xn)
|
f(xn+1)
|
1
2
3
4
5
6
7
8
9
|
-1
3
1.8
1.84319
2.10932
1.96752
1.99423
2.00036
2.00000
|
3
1.8
1.84319
2.10932
1.96752
1.99423
2.00036
2.00000
2.00000
|
1.8
1.84319
2.10932
1.96752
1.99423
2.00036
2.00000
2.00000
2.00000
|
-42
18
-0.672
-0.57817
0.659
39
-0.15303
-0.02854
0.00178
-0.00002
|
18
-0.672
-0.57817
0.65939
-0.15303
-0.02854
0.00178
-0.00002
0.00000
|
-0.672
-0.57817
0.65939
-0.15303
-0.02854
0.00178
-0.00002
0.00000
0.00000
|


