untuk materi integral romberg bisa dipajari dari materi pdf berikut
integral romberg
Monday, July 17, 2017
Thursday, June 8, 2017
Kaidah Simpson
Aturan Simpson adalah suatu aturan yang digunakan untuk menghitung luas suatu kurva polinom berderajat dua p2(x) atau berderajat tiga p3(x) dengan pendekatan yaitu pendekatan menggunakan pastisi berbentuk parabola. Dalam Metode Simpson ada dua jenis yaitu Metode Simpson 1 per 3 dan Metode Simpson 3 per 8. Tapi dalam tulisan ini saya terlebih dahulu akan membahas Metode Simpson 1 per 3.
Aturan Simpson 1 per 3 ini mempartisi kurva polinom berderajat dua p2(x) dengan 3 titik, 5 titik, 7 titik dan seterusnya sedemikian sehingga ruang partisi yang dibentuk berjumlah genap.
Perhatikan gambar diatas, misal kita menggunakan f(x) = Ax2 + Bx + C dengan tiga titik partisi yaitu x0, x1 dan x2 dengan mengambil x0 = -h, x1 = 0 dan x2 = h. Perlu diingat bahwa partisi yang dilakukan disini dianggap sama besar untuk setiap ruang partisi.
Substitusi nilai -h, 0 dan h ke f(x), sedemikian sehingga diperoleh
(-h, f(x0))  f(a) = Ah2 – Bh + C … (i)
f(a) = Ah2 – Bh + C … (i)
(0, f(x1))  f(h) = C … (ii)
f(h) = C … (ii)
(h, f(x2))  f(b) = Ah2 + Bh + C … (iii)
f(b) = Ah2 + Bh + C … (iii)
eliminasi (i) dan (ii) :
f(x0) = Ah2 – Bh + C
f(x1) = C –
f(x0) – f(x1) = Ah2 – Bh … (iv)
eliminasi (iii) dan (ii) :
f(x2) = Ah2 + Bh + C
f(x1) = C –
f(x2) – f(x1) = Ah2 + Bh … (v)
eliminasi (iv) dan (v) :
f(x0) – f(x1) = Ah2 – Bh
f(x2) – f(x1) = Ah2 + Bh +
f(x0) – 2f(x1) + f(x2) = 2Ah2 … (vi)
integralkan f(x) dengan batas bawah dan batas atas masing-masing -h dan h sehingga diperoleh luas dibawah kurva.
= [ Ah3 +
Ah3 +  Bh2 + Ch] – [
Bh2 + Ch] – [ Ah3 +
Ah3 +  Bh2 – Ch]
Bh2 – Ch]
=  (Ah3 + 2Ch)
(Ah3 + 2Ch)
=  h (2Ah2 + 6C) … (vii)
h (2Ah2 + 6C) … (vii)
Substitusi (ii) dan (vi) ke persamaan (vii) :
=  h [(f(x0) – f(x1) + f(x2)) + 6f(x1)]
h [(f(x0) – f(x1) + f(x2)) + 6f(x1)]
=  h [f(x0) + 4f(x1) + f(x2)]
h [f(x0) + 4f(x1) + f(x2)]
S2(x) =  f(x) dx
f(x) dx
=  h [f(x0) + 4f(x1) + f(x2)], h =
h [f(x0) + 4f(x1) + f(x2)], h = 
Rumus Simpson 1 per 3 untuk 2 pias atau partisi menggunakan 5 titik,
S4(x) =  f(x) dx +
f(x) dx +  f(x) dx
f(x) dx
=  h [f(x0) + 4f(x1) + f(x2)] +
h [f(x0) + 4f(x1) + f(x2)] +  h [f(x2) + 4f(x3) + f(x4)]
h [f(x2) + 4f(x3) + f(x4)]
=  h [(f(x0) + f(x4)) + 4(f(x1) f(x3)) + 2f(x2)], h =
h [(f(x0) + f(x4)) + 4(f(x1) f(x3)) + 2f(x2)], h = 
Rumus Simpson 1 per 3 untuk n pias,
Sn(x) =  f(x) dx +
f(x) dx +  f(x) dx + … +
f(x) dx + … +  f(x) dx
f(x) dx
=  h [f(x0) + 4f(x1) + f(x2)] +
h [f(x0) + 4f(x1) + f(x2)] +  h [f(x2) + 4f(x3) + f(x4)] + … +
h [f(x2) + 4f(x3) + f(x4)] + … +  h [f(xn-2) + 4f(xn-1) + f(xn)]
h [f(xn-2) + 4f(xn-1) + f(xn)]
=  h [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + f(x4) + … + 2f(xn-2) + 4f(xn-1) + f(xn)], h =
h [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + f(x4) + … + 2f(xn-2) + 4f(xn-1) + f(xn)], h = 
=  h [(f(x0) + f(xn)) + 4
h [(f(x0) + f(xn)) + 4 f(xi) + 2
f(xi) + 2 f(xi)]
f(xi)]
Contoh :
Hitunglah I =  ex dx menggunakan Metode Simpson 1 per 3 dengan 4 pias.
ex dx menggunakan Metode Simpson 1 per 3 dengan 4 pias.
Penyelesaian :
h =  = 1
= 1
x0 = 0
x1 = a + h = 1
x2 = a + 2h = 2
x3 = a + 3h = 3
x4 = a + 4h = 4
S4(x) =  h [(f(x0) + f(x4)) + 4(f(x1) + f(x3)) + 2f(x2)]
h [(f(x0) + f(x4)) + 4(f(x1) + f(x3)) + 2f(x2)]
=  (1) [(e0 + e4) + 4(e1 + e3) + 2e2]
(1) [(e0 + e4) + 4(e1 + e3) + 2e2]
=  [(1 + 54.5981) + 4(2.7182 + 20.0855) + 2(7.3890)]
[(1 + 54.5981) + 4(2.7182 + 20.0855) + 2(7.3890)]
=  [55.5981 + 91.2148 + 14.778]
[55.5981 + 91.2148 + 14.778]
= 53.8636
Kaidah Titik Tengah
Aturan Titik Tengah (Midpoint Rule) hampir mirip dengan Aturan Trapezoida tapi Aturan Titik Tengah menggunakan pendekatan Luas Persegi Panjang.
Kurva yang dipartisi sedemikian sehingga setiap partisi yang berbentuk
kurva lengkung didekatkan dengan suatu garis singgung, dimana garis
singgung yang digunakan melalui titik tengah dari lengkungan kurva pada
setiap partisi. Untuk menghitung luas dibawah kurva didekatkan dengan Luas Persegi Panjang.
 f(x)
f(x)  h.f(a +
h.f(a +  h) = M1(f)
h) = M1(f)
Jika kita memiliki sebuah partisi kurva seperti diatas dengan titik koordinat awal x0 = a dan titik koordinat ujung x1 = b = a + h maka koordinat titik tengahnya xm1 = a +  h dengan h = b – a. Maka luas dibawah kurvanya
h dengan h = b – a. Maka luas dibawah kurvanya
Jika kita mempartisi kurva menjadi dua partisi yaitu x0 = a, x1 = a + h dan x1 = a + h, x2 = b = a + 2h. Maka titik tengah dari masing-masing partisi adalah xm1 = a +  h dan xm2 = a +
h dan xm2 = a +  h dengan h =
h dengan h =  . Sehingga luas dibawah kurvanya diperoleh
. Sehingga luas dibawah kurvanya diperoleh
M2(f) = hf(a +  h) + hf(a +
h) + hf(a +  h)
h)
= h[f(a +  h) + f(a +
h) + f(a +  h)]
h)]
Sehingga Rumus Aturan Titik Tengah untuk n partisi apabila ditulis secara umum, diperoleh :
Mn(f) = h.f(a +  h) + h.f(a +
h) + h.f(a +  h) + … + hf(a + (n –
h) + … + hf(a + (n –  )h)
)h)
= h  f(a + (n –
f(a + (n –  )h)
)h)
dengan h = 
Contoh :
Hitung hasil  (2 + cos[2
(2 + cos[2 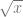 ]) dx menggunakan Aturan Titik Tengah dengan 4 dan 8 partisi.
]) dx menggunakan Aturan Titik Tengah dengan 4 dan 8 partisi.
Penyelesaian :
Untuk 4 partisi :
h =  =
= 
M4(f) = h[f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h)]
h)]
=  [f(0 +
[f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  )]
)]
=  [f(
[f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( )]
)]
=  [2 + cos[2
[2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ]]
]]
=  [2 + cos[
[2 + cos[ ] + 2 + cos[
] + 2 + cos[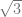 ] + 2 + cos[
] + 2 + cos[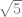 ] + 2 + cos[
] + 2 + cos[ ]]
]]
=  [8 + 0.54030 – 0.16055 – 0.61727 -0.87956]
[8 + 0.54030 – 0.16055 – 0.61727 -0.87956]
= 3.44146
Untuk 8 partisi :
h =  =
= 
M8(f) = h[f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h)]
h)]
=  [f(0 +
[f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  )]
)]
=  [f(
[f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( )]
)]
=  [2 + cos[2
[2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ]]
]]
=  [16 + cos[
[16 + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ]]
]]
=  [16 + 0.76024 + 0.33918 – 0.01034 – 0.29555 – 0.52313 – 0.69929 – 0.82978 – 0.91989]
[16 + 0.76024 + 0.33918 – 0.01034 – 0.29555 – 0.52313 – 0.69929 – 0.82978 – 0.91989]
= 3.45536
Subscribe to:
Comments (Atom)

