Jika kita memiliki sebuah partisi kurva seperti diatas dengan titik koordinat awal x0 = a dan titik koordinat ujung x1 = b = a + h maka koordinat titik tengahnya xm1 = a +  h dengan h = b – a. Maka luas dibawah kurvanya
h dengan h = b – a. Maka luas dibawah kurvanya
Jika kita mempartisi kurva menjadi dua partisi yaitu x0 = a, x1 = a + h dan x1 = a + h, x2 = b = a + 2h. Maka titik tengah dari masing-masing partisi adalah xm1 = a +  h dan xm2 = a +
h dan xm2 = a +  h dengan h =
h dengan h =  . Sehingga luas dibawah kurvanya diperoleh
. Sehingga luas dibawah kurvanya diperoleh
M2(f) = hf(a +  h) + hf(a +
h) + hf(a +  h)
h)
= h[f(a +  h) + f(a +
h) + f(a +  h)]
h)]
Sehingga Rumus Aturan Titik Tengah untuk n partisi apabila ditulis secara umum, diperoleh :
Mn(f) = h.f(a +  h) + h.f(a +
h) + h.f(a +  h) + … + hf(a + (n –
h) + … + hf(a + (n –  )h)
)h)
= h  f(a + (n –
f(a + (n –  )h)
)h)
dengan h = 
Contoh :
Hitung hasil  (2 + cos[2
(2 + cos[2 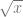 ]) dx menggunakan Aturan Titik Tengah dengan 4 dan 8 partisi.
]) dx menggunakan Aturan Titik Tengah dengan 4 dan 8 partisi.
Penyelesaian :
Untuk 4 partisi :
h =  =
= 
M4(f) = h[f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h)]
h)]
=  [f(0 +
[f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  )]
)]
=  [f(
[f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( )]
)]
=  [2 + cos[2
[2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ]]
]]
=  [2 + cos[
[2 + cos[ ] + 2 + cos[
] + 2 + cos[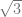 ] + 2 + cos[
] + 2 + cos[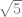 ] + 2 + cos[
] + 2 + cos[ ]]
]]
=  [8 + 0.54030 – 0.16055 – 0.61727 -0.87956]
[8 + 0.54030 – 0.16055 – 0.61727 -0.87956]
= 3.44146
Untuk 8 partisi :
h =  =
= 
M8(f) = h[f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h) + f(a +
h) + f(a +  h)]
h)]
=  [f(0 +
[f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  ) + f(0 +
) + f(0 +  )]
)]
=  [f(
[f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( ) + f(
) + f( )]
)]
=  [2 + cos[2
[2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ] + 2 + cos[2
] + 2 + cos[2  ]]
]]
=  [16 + cos[
[16 + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ] + cos[
] + cos[ ]]
]]
=  [16 + 0.76024 + 0.33918 – 0.01034 – 0.29555 – 0.52313 – 0.69929 – 0.82978 – 0.91989]
[16 + 0.76024 + 0.33918 – 0.01034 – 0.29555 – 0.52313 – 0.69929 – 0.82978 – 0.91989]
= 3.45536

No comments:
Post a Comment