Aturan Simpson adalah suatu aturan yang digunakan untuk menghitung luas suatu kurva polinom berderajat dua p2(x) atau berderajat tiga p3(x) dengan pendekatan yaitu pendekatan menggunakan pastisi berbentuk parabola. Dalam Metode Simpson ada dua jenis yaitu Metode Simpson 1 per 3 dan Metode Simpson 3 per 8. Tapi dalam tulisan ini saya terlebih dahulu akan membahas Metode Simpson 1 per 3.
Aturan Simpson 1 per 3 ini mempartisi kurva polinom berderajat dua p2(x) dengan 3 titik, 5 titik, 7 titik dan seterusnya sedemikian sehingga ruang partisi yang dibentuk berjumlah genap.
Perhatikan gambar diatas, misal kita menggunakan f(x) = Ax2 + Bx + C dengan tiga titik partisi yaitu x0, x1 dan x2 dengan mengambil x0 = -h, x1 = 0 dan x2 = h. Perlu diingat bahwa partisi yang dilakukan disini dianggap sama besar untuk setiap ruang partisi.
Substitusi nilai -h, 0 dan h ke f(x), sedemikian sehingga diperoleh
(-h, f(x0)) 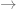 f(a) = Ah2 – Bh + C … (i)
f(a) = Ah2 – Bh + C … (i)
(0, f(x1)) 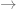 f(h) = C … (ii)
f(h) = C … (ii)
(h, f(x2)) 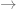 f(b) = Ah2 + Bh + C … (iii)
f(b) = Ah2 + Bh + C … (iii)
eliminasi (i) dan (ii) :
f(x0) = Ah2 – Bh + C
f(x1) = C –
f(x0) – f(x1) = Ah2 – Bh … (iv)
eliminasi (iii) dan (ii) :
f(x2) = Ah2 + Bh + C
f(x1) = C –
f(x2) – f(x1) = Ah2 + Bh … (v)
eliminasi (iv) dan (v) :
f(x0) – f(x1) = Ah2 – Bh
f(x2) – f(x1) = Ah2 + Bh +
f(x0) – 2f(x1) + f(x2) = 2Ah2 … (vi)
integralkan f(x) dengan batas bawah dan batas atas masing-masing -h dan h sehingga diperoleh luas dibawah kurva.
= [ Ah3 +
Ah3 +  Bh2 + Ch] – [
Bh2 + Ch] – [ Ah3 +
Ah3 +  Bh2 – Ch]
Bh2 – Ch]
=  (Ah3 + 2Ch)
(Ah3 + 2Ch)
=  h (2Ah2 + 6C) … (vii)
h (2Ah2 + 6C) … (vii)
Substitusi (ii) dan (vi) ke persamaan (vii) :
=  h [(f(x0) – f(x1) + f(x2)) + 6f(x1)]
h [(f(x0) – f(x1) + f(x2)) + 6f(x1)]
=  h [f(x0) + 4f(x1) + f(x2)]
h [f(x0) + 4f(x1) + f(x2)]
S2(x) =  f(x) dx
f(x) dx
=  h [f(x0) + 4f(x1) + f(x2)], h =
h [f(x0) + 4f(x1) + f(x2)], h = 
Rumus Simpson 1 per 3 untuk 2 pias atau partisi menggunakan 5 titik,
S4(x) =  f(x) dx +
f(x) dx +  f(x) dx
f(x) dx
=  h [f(x0) + 4f(x1) + f(x2)] +
h [f(x0) + 4f(x1) + f(x2)] +  h [f(x2) + 4f(x3) + f(x4)]
h [f(x2) + 4f(x3) + f(x4)]
=  h [(f(x0) + f(x4)) + 4(f(x1) f(x3)) + 2f(x2)], h =
h [(f(x0) + f(x4)) + 4(f(x1) f(x3)) + 2f(x2)], h = 
Rumus Simpson 1 per 3 untuk n pias,
Sn(x) =  f(x) dx +
f(x) dx +  f(x) dx + … +
f(x) dx + … +  f(x) dx
f(x) dx
=  h [f(x0) + 4f(x1) + f(x2)] +
h [f(x0) + 4f(x1) + f(x2)] +  h [f(x2) + 4f(x3) + f(x4)] + … +
h [f(x2) + 4f(x3) + f(x4)] + … +  h [f(xn-2) + 4f(xn-1) + f(xn)]
h [f(xn-2) + 4f(xn-1) + f(xn)]
=  h [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + f(x4) + … + 2f(xn-2) + 4f(xn-1) + f(xn)], h =
h [f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + f(x4) + … + 2f(xn-2) + 4f(xn-1) + f(xn)], h = 
=  h [(f(x0) + f(xn)) + 4
h [(f(x0) + f(xn)) + 4 f(xi) + 2
f(xi) + 2 f(xi)]
f(xi)]
Contoh :
Hitunglah I =  ex dx menggunakan Metode Simpson 1 per 3 dengan 4 pias.
ex dx menggunakan Metode Simpson 1 per 3 dengan 4 pias.
Penyelesaian :
h =  = 1
= 1
x0 = 0
x1 = a + h = 1
x2 = a + 2h = 2
x3 = a + 3h = 3
x4 = a + 4h = 4
S4(x) =  h [(f(x0) + f(x4)) + 4(f(x1) + f(x3)) + 2f(x2)]
h [(f(x0) + f(x4)) + 4(f(x1) + f(x3)) + 2f(x2)]
=  (1) [(e0 + e4) + 4(e1 + e3) + 2e2]
(1) [(e0 + e4) + 4(e1 + e3) + 2e2]
=  [(1 + 54.5981) + 4(2.7182 + 20.0855) + 2(7.3890)]
[(1 + 54.5981) + 4(2.7182 + 20.0855) + 2(7.3890)]
=  [55.5981 + 91.2148 + 14.778]
[55.5981 + 91.2148 + 14.778]
= 53.8636

No comments:
Post a Comment